三相発電機(同期機)の理論 その9
28.1 発電機の各種リアクタンスの測定法
前々回 No.26 では発電機の dq0 等価回路の dq 軸リアクタンス x"_d, x'_d, x_d, x"_q, x'_q = x_q 短絡時定数 T"_d, T'_d, T_d等を解説しました。 そして前回No.27 では私たちが系統の短絡故障計算や動 態安定度計算などで発電機正相等価回路のリアクタンス1 x として無造作に x"_d, x'_d, x_d を使い、 また逆相等価回路のリアクタンスは x₂=(x"_d+x"_q)/2などとしていることについてその根拠を詳 しく解説しました。今回はこれらリアクタンスの測定法と、発電機の無負荷飽和曲線・短絡曲 線,さらに短絡比CSR等について解説します。

28.1.1 d 軸同期リアクタンス の測定法と短絡比CSR
まずは図28.1 について解説します。発電機が三相短絡状態の場合と開放状態の場合の2 通りに ついて電圧計 V と電流計 A で測定を実施します。
始めに、図28.1(b)のように abc 相端子を三相短絡状態にして無励磁状態で回転を開始し、定格 速度に達したところでその速度を維持します。 その状態で外部電源電圧 e_fd の課電を開始して 励磁電流 i_fd をゼロから徐々に増やしていくと端子(相対地)電圧 e_a は直線的に増加していきます。 こうして図28.1(a)に示す 3 相短絡電流特性（あるいは短絡曲線）が求められます。そして端子 電圧が定格値 e_arate=1.0 に達した時の励磁電流 _shorti_fd を測定します。
次には図28.1(d)のように三相端子が開放状態で無励磁で測定を開始します。 この状態で起動 を開始して定格速度を維持します。そして界磁回路の励磁電流 i_fd を徐々に増加していくと端子 電圧 e_a （三相平衡実効値表現）も増加してやがて定格電圧 e_arate=1.0 に達します。 発電機 の“無負荷励磁特性”が図28.1(a)のように描けます。 はじめのうちは電圧は直線的に増加し ていきますが電圧が0.8 程度に達したあたりから飽和が始まるので“無負荷飽和曲線”などと も称します。端子電圧が1.0 の状態での励磁電流を _sati_fd （飽和値）を測定します。 また想定 された飽和曲線の飽和を無視して直線の無負荷励磁特性(非飽和)とした場合の励磁電流 _nonsati_fd (不飽和値)も図式的に算出しておきます。
さて、JEC やIEC などの規格ではこのように端子が短絡状態と開放状態の二通りの方法で求め た励磁電流値を使って を次式で求めるとしています。



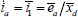
発電機の端子三相短絡時の電流は となるので短絡比という言葉の意味もうなず けますね。また、リアクタンスの測定法も先に勉強した dq0 等価回路を基礎としていることが理解できますね。
  無負荷飽和曲線に話を戻して、物理的な視点から補足します。無負荷状態では e_a が0.8 程度 以内の大きさまでは e_a と i_fd は比例関係にあるが、e_a が0.8 あたりを超えて上昇すると鉄心部 の磁気飽和の影響で磁気抵抗が増大して、電圧 Δe_a を上昇させるのに必要な界磁起電力 Δi_a （すなわちa a Δi_a/Δe_a ）が増加する。発電機のステータ＆ロータの鉄心が飽和しはじめると鉄心 以外の部位(クザビ等の金属部位)の磁束が急増して渦電流が増加します。その結果発電機の各 種リアクタンス値は磁気回路の飽和域では10％程度小さくなるのです。その小さくなる割合を 飽和率(or 飽和係数)σ と名付けています。 典型的な飽和係数を表28.1 に示します。




  さて、発電機のリアクタンスには不飽和値とそれより少し小さい飽和値の二通りがあること を説明しました。　そして実際の短絡故障計算やその他の解析で飽和値と不飽和値のどちらを 採用するかという疑問にぶつかります。　私はそういう質問をいただく度に次のよう逆質問を します。　「今行っている解析で貴方は楽観的な解と悲観的(安全サイド)な解のどちらが欲し いですか？　もちろん安全サイドですね。　それならば安全サイドになる方を採用すればよい のです」と。　要するにルールはないのです。　安全サイドの解を期待するならばそのように 選べばよいのです。　そうすると解析の目的によって例えば下記のように使い分けをすること になりますね。
遮断器の短絡容量の解析のための故障計算や負荷電流解析：
      ⇒　大き目の電流値を期待して飽和値を採用。
電力ケーブルの所要電流容量の解析のための故障計算や負荷電流解析：
      ⇒　大き目の電流値を期待して飽和値を採用。
安定度計算：　⇒シビア目の解析を期待して不飽和値を採用
高調波解析：　⇒高調波が大きめに生ずる飽和値を採用
保護リレー協調の解析：⇒　飽和値の場合と不飽和値の場合の差がどの程度になるかを確かめて判断する。



28.1.2　逆相リアクタンス の測定法
  次には逆相リアクタンス と零相リアクタンス も仕様に含まれる数値ですから当然工場出 荷時に測定して仕様通りであることを示す必要があります。 実際の測定は図28.3 のような回 路を構成して実測します。


  図 28.3(a)のように a 相端子は開放, b, c 相端子は短絡接続にしたうえで発電機を定格速度に 保ちます。 この回路は bc 相2 線短絡の回路です(補足１参照)。 次に励磁電流　i_fd を徐々に増 加して i_b=-i_c が定格電流値の 10%程度に達した状態で v_ab とを電圧計V で、また i_b(=-i_c) を電 流計 A で実測します。このの V と A の測定値は対称座標法の2 線短絡のケース（No.11 を参照） を援用して次式で表現できます。




図(a)の回路で測定した V と A の値を使って式(28.6)で を計算できることになります。

28.1.3　零相リアクタンス の測定法
  今度は図28.3(b)の回路で電圧計 V と電流計 A の値を測定します。これは bc 相2 線地絡の回 路ですから対称座標法の2 線地絡のケース(補足2 参照)を援用して


電圧計 V と電流計 A の測定値を使って を求めることができました。

  補足 1） b,c 相 2 線短絡の場合の等価回路図と式は下記の如くとなり式でした。




  今回はここまで。次回は発電機を P−Q 座標で表現する能力曲線等について解説します。今 までは主として電圧 v , 電流 i , 磁束 φ の切り口から解説してきましたが、これからは有効電力 P と無効電力Q の特性としての解説が主体になります。より実戦的なテーマになりますからご期 待ください。

(2022年4月5日　長谷良秀 記)