電気技術解析記述法発展史（その8）
19世紀電気技術史のクライマックス,Maxwellの登場(その2)

  前回は“Maxwellの四つの式”についてそれぞれの形式とその物理的な意味について解説しまし た。 今回はこれらの式より電磁波の姿を示す波動方程式が導かれ、さらに電磁波の波としての 姿を示す過程を追ってMaxwell が達成した世紀の大偉業について説明します。 今回も方程式ばか りになりましたが精いっぱいわかり易く書いたつもりです。皆さん頑張ってお付き合いください。 なおMaxwellのミニ伝記は次回へ繰り越しとします。

58.1 Maxwellの四っの式
前回のNo.57で示したMaxwell の四つの方程式を新たな式番で再録します。
微分形式の表現


あるいは
積分形式の表現



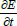
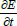
  Gaussの第1式は電界 E について、第2式は磁界 B について述べています。Faradayの第3式は電 場 E と磁場 B を関係付けています。 Ampere-Maxwellの第4式もそれぞれに E と B を関係付け ています。 Maxwellは変位電流 という概念をAmpereの式に加えて第4式を示しました。何し ろ科学者の多くがエーテル探しに没頭していた時代ですから「何もない真空空間に“ある種の電流 が流れる”と考える」こと自体が破天荒で当時の科学界の常識をぶち壊す発想でした。 Maxwell の変位電流項 が追加されたことによって第4式も E と B を関係付ける式となりました。 そのおかげで第3式と第4式が E と B の2変数連立方程式となって E=・・・, B=・・・ のようにそれぞ れ時間関数として解くことができるようになりました。 1864年当時にMaxwellが示した思考過程 をトレースする気分で式(58.1c,d)による E と B の連立方程式を解いてみましょう。

58.2 Maxwell四つの式から波動方程式の導入
  真空空間の任意の点 P(x,y,z) の電場 E(E_x,E_y,E_z,t) および磁場 B(B_x,B_y,B_z,t) として、 Maxwell第3，4式の連立方程式は次式となります。 なお、点 P(x,y,z) には電荷 Q が存在しない ので電流も存在せず としています。

時間 t は任意扱いをして、電場 E(E_x,E_y,E_z) と磁場 B(B_x,B_y,B_z) に関する次式を連立方程式とし て扱います。


上式の をフルバージョンで書けば(前回No.57で説明しました)



したがって式(58.3a)を丁寧に書き代えれば次式をえます。


上記の連立方程式の B を消去して E の式を導くこととします。式(58.3a)の両辺の回転を求めると

右辺に式(58.3a②)を代入して書き代えると


E(E_x,E_y,E_z) のみの式(58.4a)が求められましたがこれでは意味がはっきりしませんので rot(rotE) の書き代えを行います。

回転の回転 rot(rotA) に関する公式を備考58.1において証明付きで示しておきました。その結果 を利用して、ベクトル E(E_x,E_y,E_z) に関する回転の回転 rot(rotE) は次のようになります。


上式の右辺第1項に現れた に注目します。電場の任意の一点 (x,y,z) にお ける電場の強さが E(E_x,E_y,E_z) であるとして、divE はその点から湧き出す（発散する）電場量 （スカラー値）を示していいます。 ところで今考えている (x,y,z) 空間には電荷がない (Q=0) としているので Gauss 電場則で divE=0 です。



従って式（58.4b）はその右辺第1項はゼロとなり、右辺第2項のみが残ります。
結局、式(58.4a)は次式のように書き代えられました。

xyz軸成分毎に表せば


電場に関する特性が波動方程式の形で求められました。

  全く同じプロセスで（ divB=0 であることにも留意して）磁場の特性を示す波動方程式が 同形で求められます。

ただしMKSA有理単位法により

今、真空空間の座標起点 P₀(0,0,0) として任意の点 P(x,y,z) の電磁場の特性を示す式として上式が成立しています。

式(58.5c)で明らかになった偏微分方程式 は理学工学の様々な現象を説明す る基本式として登場する“波動方程式”です。

58.3 波動方程式の解から電磁波の姿を考察する
  電磁波の姿をこの波動方程式で可視化したのは勿論 Maxwell ですが、波動方程式自体は18世紀 の数学において登場して、大数学家 Jean Le Rond dʻAlembert （ダランベール1717-1783） がその一 般解を示していました。

  式(58.7c,d)に対するｄʻAlembertの一般解は次式となります。

式(58.5c)の解：


式(58.6c)の解：


式(58.5c)から式(58.8a)を求める方法は数学家に任せるとして、式(58.8a)が式(58.5c)の解である ことは式（58.8a）を(58.5c)代入してみればすぐに理解できます。皆さん確かめてみてください。
  さてここで E_x=E_xf(x-ct)+E_xb(x+ct) の意味について考えます。 E_x は E_x1(x-ct) と E_x2(x+ct) の二つの同形関数の和として表現できることを意味しています。 ところで式中の 変数 x[m] は距離であるから ct[m] の単位も距離です。 そして t[sec] ですから は速 度の単位 c[s/m] になります。
もしも点 P(x,y,z) で観測する電位 E_x1 を x 軸に沿って速さ c で x 軸方向に移動しながら観測を続け ると、観測者はいつも変わらない大きさの E_x1(x-ct) を観測することになります。 言い換えれ ば、 E_x1(x-ct) は x 軸方向に速さ c で進む進行波 （前進波：forward-waveといいます）の性質 を有することを示しています。 また E_x2(x+ct) は x 軸方向に速度 －c で進む進行波（後進波 backward-waveといいます）です。 y 軸, z 軸成分についても同様です。
ところで、式(58.8a,b)はAlembert解として求めた波の一般形ですが、通常の形式として次式が 得られます。

上式(58.9a,b)が波動方程式(58.5c)を満足させる解になっていることを確認してください。
  さて、 E と B がそれぞれ式(58.9a,b)の正弦波の特性を帯びていると表現できるわけですから 電磁波と云われる所以です。そして電磁波は真空空間(エーテルが無くても)を速度 c で全方位の 無限遠に向かって伝搬していくことになります。

  ところで波動とは一定の有限速度で伝搬（進行）するもものですから波は初めに起点になっ た場所（電磁波では電荷 Q の発生あるいは変化が生じた起点）の近接した場所に伝わり、さら にそのまた近接場所にと順番に伝わっていきます。 “波動の近接作用”といいます。 この時遠 方にはまだ波動は到達していません。 電磁波について言えば、電荷 +Q によって起点から放出 された E と B は速度 c で（－Qに向かって）遠方に伝搬していきますがその最前線のフロント 面（平面）があるはずです。フロント面より遠方には波はまだ届いていない。 電磁波は“平面 波”あるいは“横波”といわれる所以です。Maxwellは“電磁波を近接作用を伴う波動”であると理解 したといえるでしょう。 “架空の物質“エーテル”が存在しない真空空間において近接作用で電 場と磁場が伝搬していく”という発想は当時の科学者にはなかなか受け入れられない発想であっ たでしょう。

ここで電磁波についてその“波の性質”として重要なことを整理しておきます。
ⅰ）電場 E (ベクトル値)と磁場 B （ベクトル値）は波の進行方向に垂直である。波が z 軸方向 に進行しているならば E および B は xy 平面内にあり、かつ互いに直交関係にある。
換言すれば、電磁波の進む方向は電場 E と磁場 B のベクトル積（外積 E×B）で与えられる。
ⅱ）電磁場は横波の性質を有しており、正弦的に変化する。 また E と B は同じ波長,同じ周 波数で変化し、互いに同位相である。 E と B は不離一体の関係にあり、一方だけが存在する ことはありえない。
ⅲ）電磁波(角周波数 ω とする)が＋ z 軸方向に進行中でその位置が z、時間が t にある（すな わち P(0,0,z:t) の位置）とする。 この時、電場 E はｘ軸に平行に振動する。磁場 B は y軸 に平行に振動する(右手法則)。これによって、 E および B はそれぞれ進行方向 ｚ と時間の正 弦関数として次式のように表すことができる。

ⅳ） また、 E と B には次式の関係がある。

式(58.10a)を（58.10b）に代入して整頓すると


また次式(58.10d)に代入しても当然同じ結果を得る。 確かめてみましょう。

電場 E と磁場 B の波高値には式(58.10c,ed)の関係が成立している。
  Maxwellはこの式に登場するコンスタント c について電場 E と磁場 B の波としての伝搬速度と 考えました。 波ならば真空中でも伝搬してエネルギーを伝えることもできる・・・。 しかし この発想は当時の科学界の常識を大きく逸脱するものであり、また何よりも実証的説明になって いないので当時の科学界ではMaxwellの発想を支持する学者はごく一部に限られていたといわれます。

58.4 実際の電磁波の姿
さて、電場 E と磁場 B を伴う電磁波の姿が方程式的に見えてきました。 そこで今度はいくつか の状況を想定して電磁波の姿をより具体的にイメージしてみましょう。
Case1: 時間 t=0 に 起点 P(0,0,0) に突然電荷 Q1(t) が生じた場合
  これは図58.2のように点 P(0,0,0) にて放送局の発信アンテナから放送電波が全方位に送信 開始される場合に相当します。図58.1の送信用アンテナをイメージして下さい。 送信アンテ ナから送り出された電磁場 E と B は全方向に速度 ｃ で拡散していきます。 言い換えれば、 任意の方向の距離 r に対して電場 E(r-ct) 磁場 B(r-ct) の形で拡散（進行）します。 x 軸 方向には E(x-ct),y 軸方向には E(y-ct),z 軸方向には E(z-ct) の姿で進行することになります。

図58.3は x 軸方向に向かう電磁波の E と B に関するスナップショットです。


Case2: 座標起点 P(0,0,0) に正電荷 +Q が存在する場合
  既に或る大きさの電荷 +Q が定常的に存在するのですから原点から距離 r<ct 以内の大きさ のガウス空間内を考えれば、どの部位にも静電磁場 E と B が満たされて存在します。
E(x,y,z:t), B(x,y,z:t) と表すことにすれば、これは時間的に変化しない静磁場なので δE/δt=0, δE/δt=0 です。
他方で r>ct の超遠方領域に想いを致せば、この 領域にはまだ電磁波は届いていません。この領域に向かって電波のフロント平面波 E(r-ct), B(r-ct) が速度cで拡散進行中です。

Case3: 座標起点 P(0,0,0) にて変調周波数 f=ω/2π の信号電場が発信される場合。
  これはCase2で点 P(0,0,0) にて発信される電荷 +Q が角周波数 ω で Qsinωt のように変化 する（変調される）場合に相当します。搬送周波数 f=ω/2π の電波発信です。

当該電波塔がカバーする距離受信可能な圏内、例えば電波塔から100km圏内 r≅100km≪cx1sec=3x10⁸[m] においては電波は事実上瞬時に全域をカバーするので近似 的な意味で全域に一様に E(ωt), B(ωt) として届くことになります。電波速度は 300[m/μs] ですから 100km 遠方への伝搬時間は 330μsec で“事実上瞬時”といえるので伝搬時間遅れを意 識する必要はありません。
  しかしながら物理学的な視点での r>ct rct>の超遠方領域においてはまだ電磁波は届いておらず、 フロントの平面波が速度 c の電磁波 |E(0,0,0:t=0)|(r-ct) および |B(0,0,0:t=0)|(r-ct) として無限遠に向かって全方位で拡散進行中であるといえるでしょう。

Case4: z 軸方向に張られた送電線の起点方向 P(0,0,0) からサージがz方向に進行する場合。
  線路用遮断器の併入あるいは雷撃によってstep状のサージ電圧がz軸方向の送電線を速度 c で進行する場合です。線路が非減衰であるとすれば E1(t)で、また線路の減衰特性を考慮すれ ば Ee^-α1(t) の波形で進行します。 この場合、いわゆる“電荷 Q の行列”が速度 c で導体内を z 方向に進みます。その先頭の電荷 Q₁ は xy 断面に電磁場 E(x,y) B(x,y) のフロント平面波とな ります。

  送電線の或る位置の点 P(0,0,z) にある電荷 Q はその xy 断面に電磁場 E(x,y,z), B(x,y,z) を伴います。 そしてこの電磁波は xy 断面の任意の距離 r では E(r-ct,z), E(r-ct,z) の波 形で拡散していきます。 特に x 軸方向に注目すれば E(x-ct,0,z), B(x-ct,0,z) で進行中と 表すこともできるでしょう。

Case5: z軸の送電線に定常電流 i=dQ/dt が流れている場合
  送電線の任意の位置 P(0,0,z) の電荷 Q はあくまでその点 P と直交する xy断面に電場 E 磁場 B をつくります。 ただ私たちの扱う送電線近傍の電磁場の範囲は勿論 r≪cx1sec=3x10⁸[m] ですから、その範囲内のガウス閉面内では電磁場は事実上瞬時の現 象として考えればよいことになります。 直流電流の場合も交流電流の場合でもこの事情はか わりません。

さて、Maxwellの電磁波解説は前回No.57でA4サイズ22頁に加えて今回も14頁にわたる方程式の羅 列となりました。 Maxwell の発想した電磁波理論の一通りの解説にはやはりこの程度の紙面が 必要ということでしょう。
“わかり易く”を心掛けたつもりですが果たして皆さんにご理解いただけたかどうか？不安気分です 。 私のe-addに率直な感想などをお聞かせいただければ幸甚です。

hasey:@jcom.home.ne.jp
次回No.59ではMaxwellのミニ伝記とHerzによる電磁波の実証実験について記したいと思っていま す。 電気が物理科学から実用工学に転換する20世紀が目前のところまで来ました。

＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊

備考58.1: 発散 divA=∇A, 回転 rotA=∇xArotA,勾配 gradB=∇B の解説

はじめに演算子の表記法について示しておきます。


なお k₁, k₂, k₃ はそれぞれ x,y,z 軸方向を向く大きさが1の単位ベクトルです。
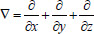
なお、ナブラ記号 ∇ はベクトル演算子です。なお k₁, k₂, k₃ を略して単に で表す ことがあります。
ベクトル A(A_x,A_y,A_z) に対して ∇xA は ∇ と A の外積(ベクトル積)です。
∇・A は ∇ と A の内積(スカラー積)を表します。

(a)発散の定義: 発散 divA=∇A
発散については前回No.57.1備考で説明しました。その復習をします。

ベクトル場において、ベクトル A(A_x,A_y,A_z) の発散 divA は次式で定義されます。 divA はスカラ ー値です。

∇A はスカラー値でベクトル演算子 ∇A とベクトル A(A_x,A_y,A_z) の内積 ∇・A と考えることもでき ます。

(b)回転の定義: rotA=∇xA
ベクトル A の回転 rotA は次式で定義されます。 rotA もベクトル値です。回転については既に No.57.xxで一度解説しましたのでおさらいです。

rotA は ∇ と A との外積 ∇ × A と考えることもでき、ベクトル値です。
なお、 A が ｚ 軸方向のベクトル A(0,0,A_z) とすれば、ベクトル rotA は A の方向 z 軸と直交して xy 平面のどこかにあり、 rotA=A'(A'_x,A'_y,0) となります。

(c)回転の回転: rot(rotA)
Maxwellの第3，4式を連立方程式として解く過程で登場する回転の回転 rot(rotA) について解説し ます。 ベクトル A(A_x,A_y,A_z) に対して rotA はベクトルであり、したがって rot(rotA) もベク トルです。 なお、 A が ｚ 軸方向のベクトル A(0,0,A_z) とすればベクトル rotA=A'(A'_x,A'_y,0) は A の存在する z 方向と直交して xy 断面のどこかにあります。 そして回転ベクトル rot(rotA)=A"(0,0,A"_z) は rotA の存在する xy 平面と直交して z 軸方向(負値であれば -z 軸向きのベク トルであるといえます。
実は次式のような公式があります。

この公式を利用すればMaxwell式は簡単に解けますが、それではあっさりしすぎるので、以下では 上記の公式を証明する形で rot(rotA) についてもう少し具体的に解説します。
ベクトル A(A_x,A_y,A_z) に対して回転ベクトル rotA は次式のように表記されるのでした。


従って回転ベクトル rot(rotA) はいささか長いですが次式のようになります。


以上で公式(58.h3)の証明ができました。
なお、A が ｚ 軸方向のベクトル A(0,0,A_z) とすれば、上式で A_x=A_y=0 ですからベクトル rot(rotA) は k₃ 方向（z軸方向）の成分のみとなることは明らかです。

(d)勾配の定義: gradB=∇B
スカラー場において、スカラー量 B(x,y,z) に対して gradB（ベクトル量）が次式で定義されま す。 gradB は勾配（gradient）と云いベクトル量です。


(2025年4月10日 長谷良秀 記)