対称座標法(Symmetrical Components:012 法):その2
前回のNo.7で対称座標法とは「
abc 相の複素電気量を0,1,2 相の複素変数に変換する変数変換である
こと」「その変換式に含まれる±120 度移相するVector operator a , a
2 について」の解説を行った上で変
換式・逆変換式の定義式だけを示しました。 いよいよ対称座標法の本題の解説をします。
8.1) 対称座標法の変換式と逆変換式語
対称座標法では三相回路の任意の地点の(したがって、系統の全地点の)
abc 相(
abc 領域(domain)
と称す)の電気量が012-domain の電気量に変換されます。 No.7 の最後に示した対称座標法の変換式
(7.5a)と逆変換式(7.5b)を再掲します。

スペース節約のため略記すれば

ただし

ここでa と
a は逆行列の関係にあり、両者をかけ合わせればユニット行列になります。

注1)なお行列演算(行列式の加減乗除)の基礎的事項の解説はここではしませんが、不慣れな読者は
これを機に自分のものにしてください。
上式では複素電圧
v についてのみ記していますが、電流
i ,磁束
φ 、さらには電界ε などすべての電気
量が同じ形式で
abc -領域から012-領域に変換されることを理解してください。
さて、対象としている三相回路のすべてのメンバー(発電機。変圧器・母線・送電線・配電線・負荷な
ど全て)、あるいはすべての地点においてこの変換式による
abc -領域から012-領域への変換が行われま
す。したがって回路内のどの地点においても両領域での1対1対応は保全されていることになります。
8.2) 送電線インピーダンスの012 変換
図8.1a のような送電線の任意の地点
m と
n の2 地点間の電圧・電流・インピーダンスの関係式につ
いて吟味します。ここではキャパシタンスは無視しています。

2 地点間の電位差を示す式

略記すれば

δV
aはmn地点間のa相電圧降下です。上式は図8.1a の回路を忠実に式にて表現した
abc領域の関係式
です。 この式を012 領域の式に変換する作業は簡単で式(8.1b)の
vabc=a2・v012と
iabc=a2・i012等の
変換式を各地点に当てはめて式(8.2b)に代入するだけでよいのです。

上式はすでに012 領域の式に変換された式ですが、左辺がδv
bc=の形になっていません。そこでこの
式の各辺に式(8.1c)のa を左積してみます。

a・a
2 は(8.1d)に示したようにユニット行列で a・a
2=1ですからかけてもかけなくてもかわりません。
したがって

abc 領域の式(8.2)が012 領域の式(8.3a)に変換されました。両式は同形ですが012 領域ではそのインピ
ーダンスはz
012≡a
2・z
abcaとなることがわかります。 012領域でのインピーダンス z
012はz
abcをa
2と
a でサンドイッチ挟む形で表現されることを示しています。
注) 行列式演算では
A・B≠B・Aですから掛け算の順序入れ替えは禁じ手です。
たとえば X・Y = Z 行列式に別の行列aをかけるとき 左積 a・X・Y=a・Z または右積
X・Y・a = Z・a は ok ですが、a・X・Y = Z・aは間違いです。
8.3) 三相平衡な送電線のインピーダンス
図8.1a で
abc 各相の導体配置が平衡である(撚架されている)とすれば各線の自己インダクタンスと
相間の相互インダクタンスは

となります。 この条件でz
012≡(a.z
abca
2)がどのような形になるかを計算してみます。

結局、式(8.3a)は丁寧に書けば下式となります。

式(8.2a)で送電線が3 相平衡として式(8.4)を付与すると、この3 相平衡送電線の関係式は012 領域に変
換されて式(8.6a)あるいは(8.6b)となります。 平衡線路のインピーダンス行列は012 領域では対角
線の行列素以外はすべてゼロになっています。零相回路・正相回路・逆相回路に相互インダクタンス的
なカップリングがないことを意味しています。またこの式より012 領域での等価回路として 図8.1b
を得ます。
abc 領域では各相間に相互インダクタンスがあるので各相を独立に扱うことはできません
が、012 領域に変換されると正逆零相間に相互インダクタンスがなくて、正相・逆相・零相それぞれ独
立な3 つの簡単な送電線回路になるのです。
もしも線路が多少不平衡であるとします。その場合はインピーダンス行列(8.5)の0の部分のところどこ
ろにぱらぱらと0 に近い小さな数字が入ります(sparse Matrix といいます)。正相・逆相・零相回路の間
に弱い相互インピーダンスがあるということです。 ただし不平衡度は短距離送電線では無視できる
し、長距離送電線では一般に撚架が行われるので一般の数値解析では平衡と考えて正相・逆相・零相回
路を独立として扱います。
8.3) 送電線キャパシタンス012 変換
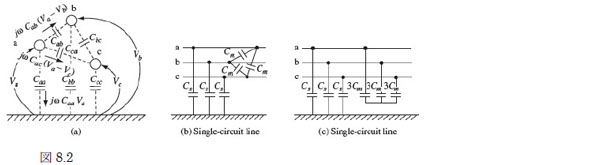
或る区間長の送電線には図8.2a のように相間と相対地間にキャパシタンスが存在します。図8.2b の
ように三相平衡とすれば、a 相から漏れ出る充電電流i
a は次式となります。

b 相, c 相についても同形ですからabc 領域での行列しとして次式が成り立ちます。

さて、abc 領域での充電電流式(8.7)を012 領域の式に変換してみてください。“習うより慣れろ”といい
ます。これは対称座標法に不慣れな皆さんへの宿題です。 変換された式が正しければ図8.2cの等価回
路図と一致するはずです。
今回はここまでで打ち止めです。 対称座標法の話はまだまだ続きます。
2020年8月15日 長谷良秀 
